Visualising Bianchi modular forms meta

2024-08-08
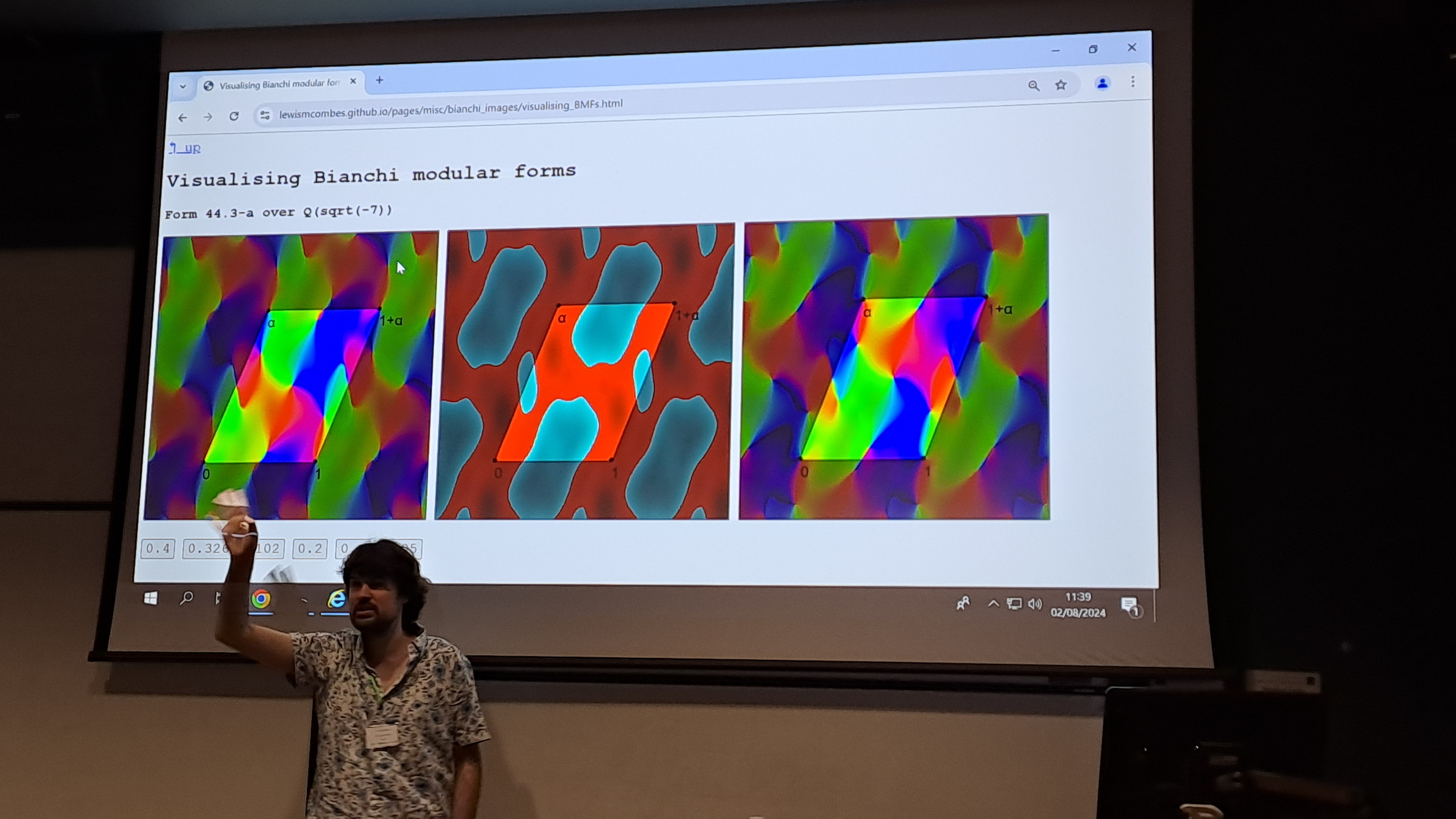
I made this toy so I could get more visual intuition for Bianchi modular forms, which are vector-valued automorphic forms for GL(2) over imaginary quadratic fields. The particular form on the page is weight 2, meaning it has 3 components. Each component is a function from hyperbolic 3-space to the complex numbers.

These plots are using the model of hyperbolic 3-space given by the upper-half space (in analogy with the upper-half plane used in the theory of classical modular forms). Each plot shows the complex value of the component in the standard way (argument is given by hue, magnitude by light/darkness). The plots are "looking down" at the copy of the complex plane sitting at the bottom of hyperbolic 3-space, at a particular height. This height can be controlled by the buttons.

The button labeled "0.3264..." is the plot of the form at height approximately 1/(88)^(1/4), where all three components appear to vanish in the middle of the fundamental parallelogram.

2024-10-22
At Y-RANT VI, I talked about Bianchi modular forms and demonstrated this toy. It was my hope to bring some interest to the study of Bianchi modular forms, as there are many unanswered questions. Below is a picture from the talk, taken by Ho Leung Fong.



At the end of this talk, inspired by Dan Fretwell's example at Y-RANT II in 2019, I distributed a poster with an explicit call to action: can anyone prove that this Bianchi form vanishes at the point (1/2 + alpha/2, 1/88^1/4)? The original poster contains a typo, claiming the form vanishes at (1+sqrt(-7))/4, when in fact the value should be (3+sqrt(-7))/4. You can download a corrected version by clicking the image below:



Up to 10 of these "super rare" uncorrected posters now hang in maths departments around the world. Can you find them all? If you download and put up one of these posters, please let me know :)